Max Cut Intergrality gap
Graph \(G\) s.t. \(\max f_g \leq s\) but \(\exists\) \(d\)-pdist \(\mu\) s.t. \({\tilde{\mathbb{E}}}_\mu f_G \geq c\).
(Bigger \(d\), larger \(c\), smaller \(s\) make gap stronger)
\(NP\)-hardness of approximation \(\Rightarrow^*\) integrality gap.
Can we obtain the reverse implication?
A priori unlikely: What if sos is not the best algorithm?
Thm: If Khot’s Unique Games Conjecture (UGC) is true then can translate any integrality gap (even for degree \(2\)) to corresponding hardness of approximation.
Moreover, generalizes for every constraint satisfaction problem.
(Khot-Kindler-Mossell-O’Donnell, Mossell-O’Donnell-Oleszkiewicz, Raghavendra)
Max Cut Integrality Gap (KKMO’04,MOO’05)
Thm: If there is a \(1-\epsilon\) vs. \(1-\delta\) gap for Max Cut, then can reduce unique games problem to distinguish given \(G\) between (i) \(\max f_G \leq 1-\epsilon+o(1)\) and (ii) \(\max f_G \geq 1-\delta-o(1)\).
Proof idea: (Generalizes to any CSP (Raghavendra ’08))
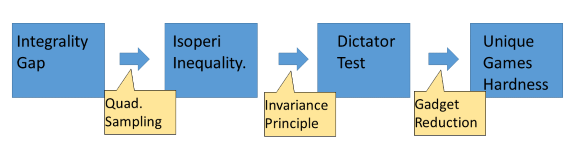
Proof outline:
\(2LIN(k)\) Problem: Given set \({\mathcal{E}}\) of equations of form \(x_i + x_j = a_{i,j} (\mod k)\), compute \({\mathop{\mathrm{val}}}({\mathcal{E}}) = \max_{x\in({\mathbb{Z}}_k)^n} \color{red}{\text{ frac. of eqs satisfied by $x$ }}\)
\(UG(\epsilon)\) Problem: Distinguish between \({\mathop{\mathrm{val}}}({\mathcal{E}}) \geq 1-\epsilon\) and \({\mathop{\mathrm{val}}}({\mathcal{E}}) \leq \exp(1/\epsilon)\) where \({\mathcal{E}}\) is \(2LIN(k=\exp(1/\epsilon^2))\) instance.
Proof outline:
KKMO: Reduce \(UG(\epsilon)\) to \(0.878 + {\mathop{\mathrm{poly}}}(\epsilon)\) Max Cut approx.
❤ of reduction: An encoding \(E:{\mathbb{Z}}_k\rightarrow{\{0,1\}}^{2^k}\) and graph \(\tilde{G}\) on \(2^k\) vertices satisfying:
Completeness: \(\forall x\in{\mathbb{Z}}_k\), \(E(x)\) is cut of value \(\alpha\) in \(\tilde{G}\).
Soundness: For every \(y\in{\{0,1\}}^{2^k}\), if \(y\) cuts \(\gt0.878\alpha+\epsilon\) edges, \(y\) is “correlated” with \(E(x)\).
Gap \(\Rightarrow\) Isoperimetry \(\Rightarrow\) Gadget
\(G=([n],E)\) s.t.
\(\max f_G \leq 1 -\epsilon\) but \({\tilde{\mathbb{E}}}_\mu f_G \geq 1-\delta\)
\(\Rightarrow\)
\((X,Y)\) over \({\mathbb{R}}^{2d}\) s.t. \({\mathbb{E}}X_iY_i \geq 1-\delta\) but \({\mathbb{E}}[\Psi(X)\Psi(Y)] \leq 1-\epsilon\) \(\forall \Psi:{\mathbb{R}}^d\rightarrow {\{0,1\}}\).
Graph \(\tilde{G}=({\{0,1\}}^d,\tilde{E})\) s.t. \(\max f_{\tilde{G}} \geq 1-\delta\) max cuts are \(\Psi_i(x)=x_i\) (\(i=1..n\)).
\(\Leftarrow\)
\((X,Y)\) over \({\{0,1\}}^{2d}\) s.t.
\({\mathbb{E}}X_iY_i \geq 1-\delta\)
Soundness of gadget: If \({\mathbb{E}}_{\{x,y\}\in \tilde{E}} (\Psi(x)-\Psi(y))^2 \geq 1 - \epsilon + \Omega(1)\) then \(\Psi \approx \Psi_i\) in sense of having influential coordinate.
Invariance Principle (MOO’05)
Central Limit Theorem: If \(\Psi:{\mathbb{R}}^d\rightarrow{\mathbb{R}}\) is a linear function with \(\Psi_i^2 \ll {\| \Psi \|}^2\) for all \(i\) then
\[ \Psi(X_1,\ldots,X_d) \approx \Psi(B_1,\ldots,B_d) \]where the \(X_i\)’s are i.i.d Gaussians in \(N(1/2,1/4)\) and the \(B_i\) are i.i.d Bernoullis in \({\{0,1\}}\).
Invariance Principle: If \(\Psi:{\mathbb{R}}^d\rightarrow{\mathbb{R}}\) is a constant degree polynomial with \(\Psi_i^2 \ll {\| \Psi \|}^2\) for all \(i\) then
\[ \Psi(X_1,\ldots,X_d) \approx \Psi(B_1,\ldots,B_d) \]where the \(X_i\)’s are i.i.d Gaussians in \(N(1/2,1/4)\) and the \(B_i\) are i.i.d Bernoullis in \({\{0,1\}}\).
\(\Psi_i^2 := {\mathbb{E}}_{X_1\ddots X_{i-1}X_{i+1}\ddots X_d} Var_{X_i} \Psi(X_1,\ldots,X_d)\)
Can drop degree assumption by “noising up” \(\Psi\).
Invariance Principle (MOO’05)
Invariance Principle: If \(\Psi:{\mathbb{R}}^d\rightarrow{\mathbb{R}}\) is a constant degree polynomial with \(\Psi_i^2 \ll {\| \Psi \|}^2\) for all \(i\) then
\[ \Psi(X_1,\ldots,X_d) \approx \Psi(B_1,\ldots,B_d) \]where the \(X_i\)’s are i.i.d Gaussians in \(N(1/2,1/4)\) and the \(B_i\) are i.i.d Bernoullis in \({\{0,1\}}\).
Corollary: Gadget \(\tilde{G}\) is sound.
Reduction outline
Transform UG instance \(\mathcal{I}\) on \({\mathbb{Z}}_k^n\) into max-cut instance \(\mathcal{G}\) on \(n\) blocks of \(2^k\) vertices. . . . (\(\mathcal{G}\) has many copies of \(\tilde{G}\) on pairs of blocks.)
Completeness: \(\Rightarrow\) If \(x\in\Sigma^n\) is “good” then \(E(x_1)\cdots E(x_n) \in {\{0,1\}}^{n2^d}\) “good” cut for most copies.
Soundness: \(\Rightarrow\) If \(\Psi:{\{0,1\}}^{n2^d}\rightarrow{\{0,1\}}\) is often “good” cut then can decode \(\Psi\) to “good” assignment \(x\).
Conjectured complexity: 3SAT
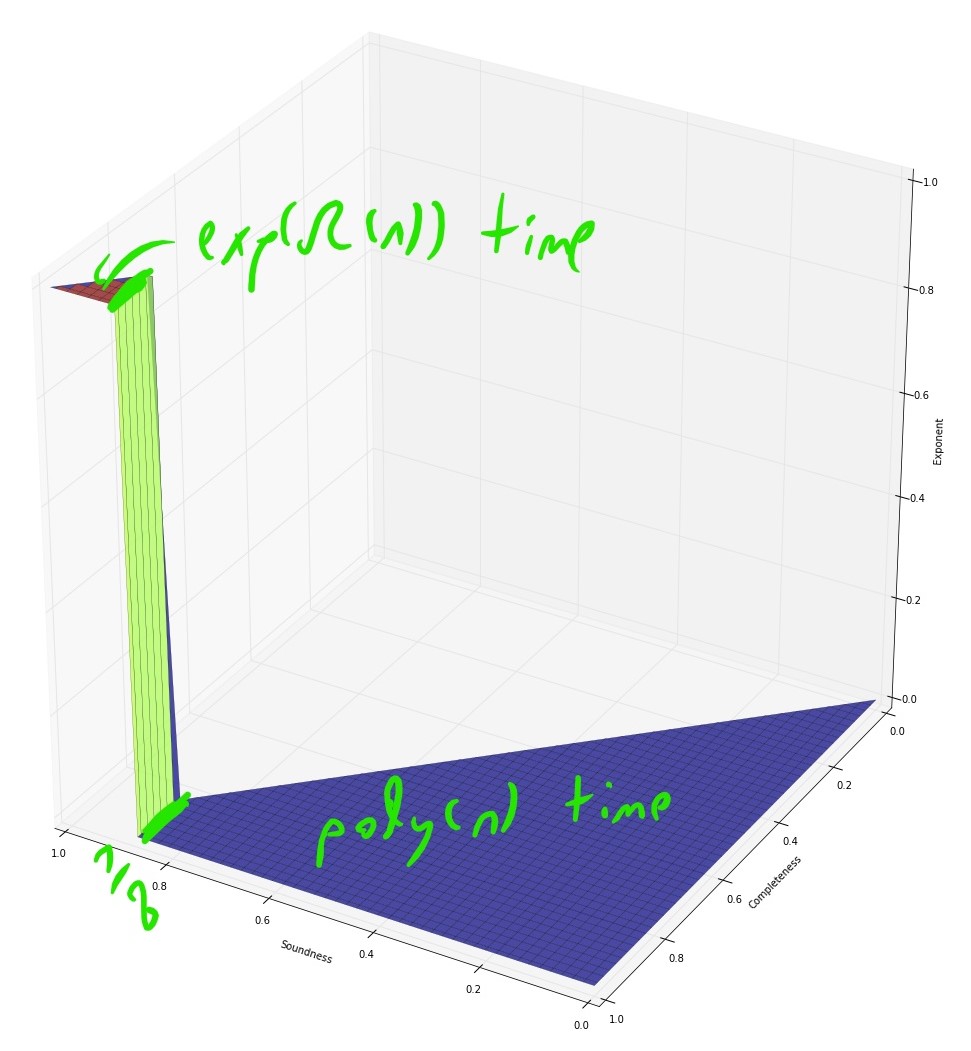
(modulo ETH)
Conjectured complexity: 3XOR
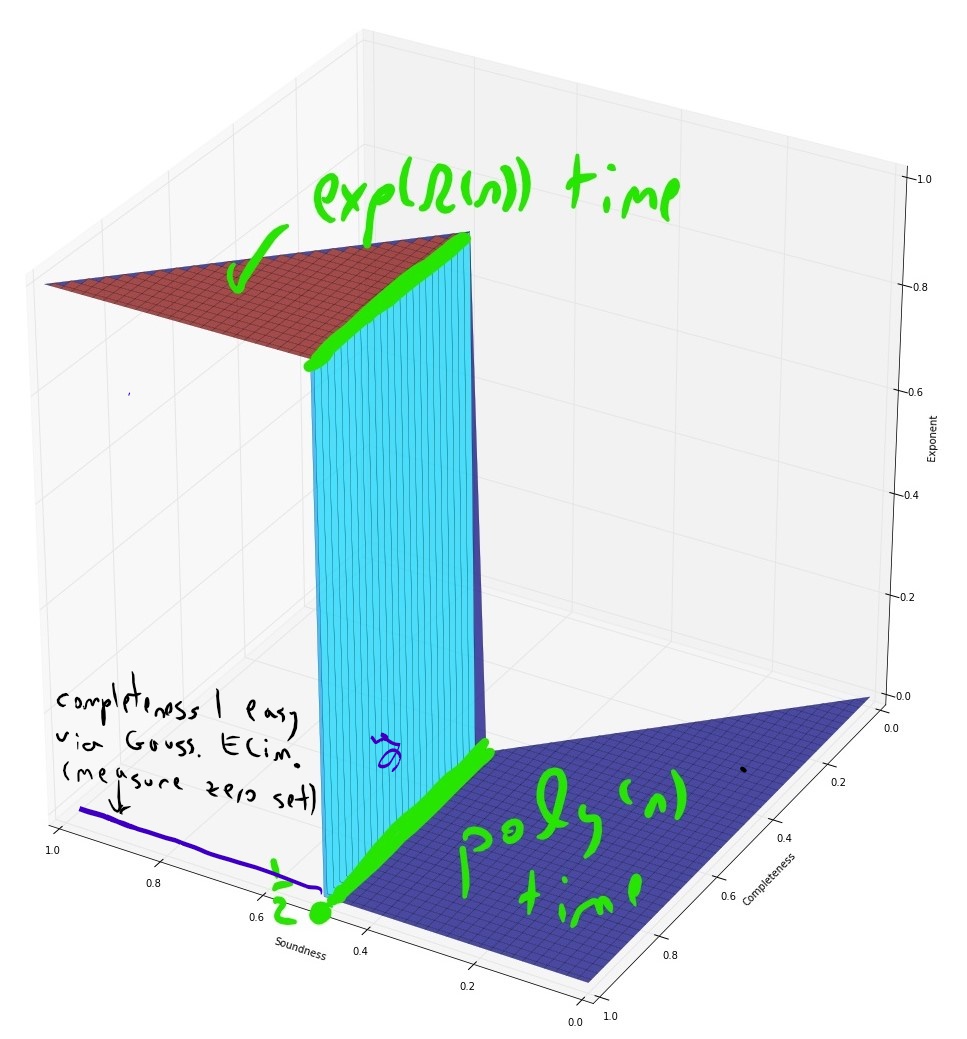
(modulo ETH)
Conjectured complexity: Max Cut
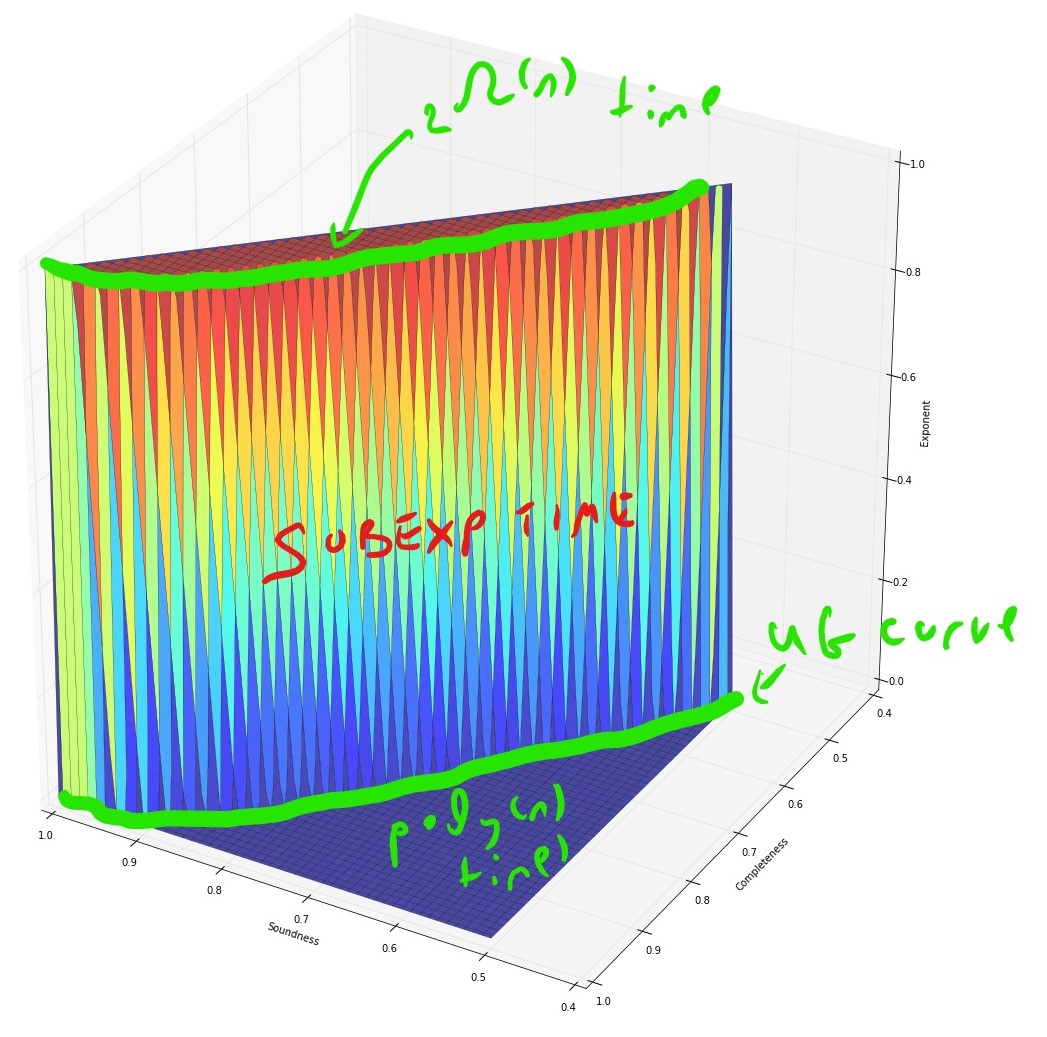
(modulo ETH, UGC, and subexp algorithm)
Summary
Assuming the UGC (basic variants of) the SOS program is optimal for a great many approximation problems.
Finite obstruction for single algorithm \(\Rightarrow\) universal hardness result.
Is the UGC true? Big open question.
Drawbacks of results we saw:
- Integrality gaps only for degree two sos.
- Hardness results only based on unique games conjecture.
- Huge quantitative losses :blowup of \(\exp(k)=\exp(\exp({\mathop{\mathrm{poly}}}(1/\epsilon)))\) from \(UG(\epsilon)\) to get \(0.878+{\mathop{\mathrm{poly}}}(\epsilon)\) hardness for max cut).
\(\epsilon \sim 0.01\) for non trivial results, reduction can’t output graphs smaller than \(\approx 2^{2^{10^4}}\) vertices.
Stronger results for other problems:
Linear degree CSP integrality gaps for sos (Grigoriev’01,Schoenebeck’08,Tulsiani’09,B-Chan-Kothari’14,…)
NP hardness results for certain CSP’s (Håstad’95,…,Chan’13)
Interestingly, these almost match up.
Bigger open question: Tight (in approx value and running time) algorithms and NP hardness results for all CSP’s.
Conjecture: SOS Algorithm is (up to \(\pm \epsilon\)) optimal approx algorithm for all CSP’s.
UGC implies partial variant of this conjecture, could be true independently of UGC.