Unique Games and Small Set Expansion
Boaz Barak and David Steurer
UCSD winter school on Sum-of-Squares, January 2017
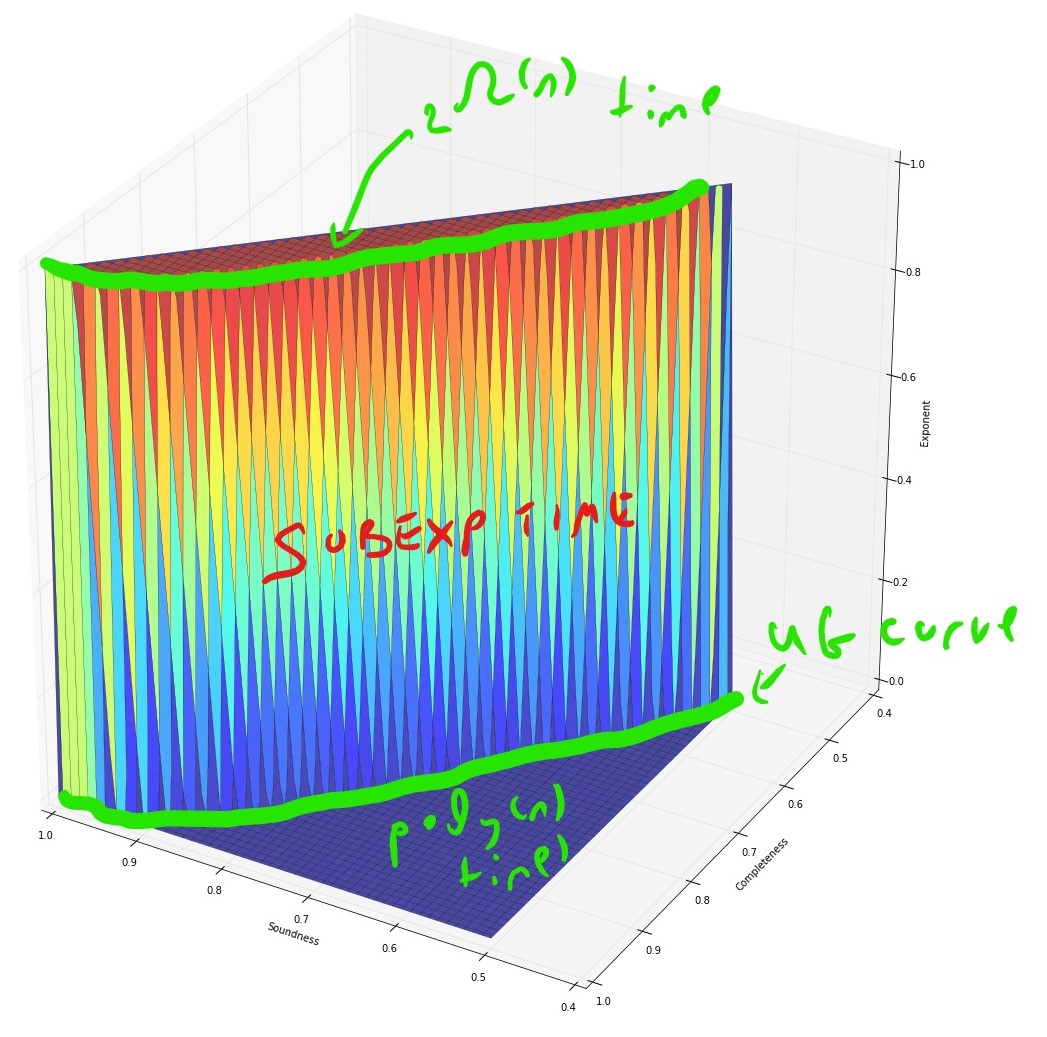
Subexponential time algorithms for Unique Games and Small Set Expansion
Unique Games Problem
\(UG(\epsilon)\) problem
Input: Set \({\mathcal{E}}\) of \(m\) eqs of form \(\{ x_i + x_j = c_{i,j} \mod k \}\).
Goal: Distinguish between \(\max {\mathcal{E}}(x) \geq 1-\epsilon\) and \(\max {\mathcal{E}}(x) \leq \epsilon\)
Unique Games Conjecture: (Khot’02) For every \(\epsilon\), \(UG(\epsilon)\) is NP hard.
(Can always choose \(k=\exp(1/\epsilon^2)\))
For eq’s involving three variables, distinguishing \(1-o(1)\) and \(1/k+o(1)\) is exponentially NP hard (Hastad, Moshkovitz-Raz)
Thm: (Arora-B-S) Can solve \(UG(\epsilon)\) in \(\exp(n^{O(\epsilon^{1/3})})\) time.
Intermediate complexity conjecture
Cor: If UGC is true, then there is a CSP \(P\) and \(c \gt s\) and \(\xi\in (0,1)\) such that fastest alg to solve \(CSP(P)_{c \text{ vs } s}\) is \(\exp(O(n^\xi ))\).
Small set expansion
Define \(G\) on \(nk\) vertices where \((i,a) \sim (j,b)\) iff \(a+b = c_{i,j}\).
Recall \(f_G(x) = \tfrac{1}{E_G} \sum_{i\sim j} (x_i-x_j)^2\)
Identify \(x\in {\mathbb{Z}}_k\) with \(\hat{x}\) in \({\{0,1\}}^{nk}\) (\(\hat{x}_{i,a}=1\) iff \(x_i=a\))
Claim: If \(x\) satisfies \((1-\epsilon)m\) equations, then \(f_G(\hat{x}) \leq \epsilon \mu(\hat{x})\).
(Def’n: \(\mu(x):={\| x \|}^2/n\) (\(=|x|/n\) if \(x\in{\{0,1\}}^n\)) )
Small set expansion
\(SSE(\epsilon)\) problem
Input: A graph \(G\).
Goal: Distinguish between \(\varphi_G(1/k)\leq \epsilon\) and \(\varphi_G(1/k) \geq 1-\epsilon\)
(\(\varphi_G(\delta):=\max_{|S|\leq \delta n} f_G(1_S)/\mu(S)\))
Natural graph problem, useful in analysis of Markov chains, etc.. etc
Small Set Expansion Hypothesis: (Raghavendra-S’12) For every \(\epsilon\), \(SSE(\epsilon)\) is NP hard.
Saw: Map \({\mathcal{E}}\leadsto G\) s.t. \(\max_{x\in{\mathbb{Z}}_k} {\mathcal{E}}(x) \geq 1-\epsilon \Rightarrow \varphi_G(1/k) \leq \epsilon\).
“Corollary”: UGC implies SSEH
Theorem: (Raghavendra-S’12) SSEH implies UGC
Structure theorem
Thm: (Arora-B-S) Can solve \(SSE(\epsilon)\) in \(\exp(n^{O(\epsilon)})\) time.
Given graph \(G\), define \(0 = \lambda_1 \leq \lambda_2 \leq \cdots \leq \lambda_n\) be eigenvalues of \(I-(1/d)A_G\).
Cheeger’s Ineq: If \(\varphi_G(1/2) \geq \epsilon\) then \(\lambda_2 \geq \Omega(\epsilon^2)\).
Structure Thm: (Arora-B-S) If \(\varphi_G(\delta) \geq 0.1\) then \(\lambda_{n^{O(\sqrt{\epsilon})}/\delta} \geq 1000\epsilon\)
Structure Thm \(\Rightarrow\) Algorithm
Given graph \(G\), define \(0 = \lambda_1 \leq \lambda_2 \leq \cdots \leq \lambda_n\) be eigenvalues of \(I-(1/d)A_G\).
Cor: For \(m=n^{O(\sqrt{\epsilon})}\), if \(\lambda_m \geq 1000\epsilon\) then \(\varphi_G(\lambda) \leq 0.1\).
Algorithm follows from following lemma:
Lemma: If \(x\in{\{0,1\}}^n\) satisfies \(f_G(x)/|x| \leq \epsilon\) and \(\lambda_m \geq 1000\epsilon\), can find \(x^*\) s.t. \(f_G(x^*) \leq 0.1\mu(x^*)\) and \(\mu(x^*) \leq 2\mu(x)\).
Search over subspace
Proof: For every \(x\), if \(\tilde{x}=x/{\| x \|} = \sum \alpha_i v_i\) then \(f_G(x)/\mu(x)=\tfrac{1}{d{\| x \|}^2}\sum_{i \sim j} (x_i-x_j)^2 = \sum_i \alpha_i^2 \lambda_i\).
So if \(f_G(x)/|x| \leq \epsilon\) and \(\lambda_{m} \geq 100\epsilon\) then \(\sum_{i\gt m} \alpha_i^2 \lt 0.001\).
Projection of \(x\) to \(Span\{ v_1,\ldots, v_m \}\) has \(0.99{\| x \|}\) norm.
\(\Rightarrow\) \(\exp(O(m))\) time algorithm to find it. ∎
Soft Cheeger’s Thm
Recall
Cheeger’s Inequality: If \(f_G(x)\leq \epsilon {\| x \|}_2^2\) then there is threshold \(S\) cut of \(x\) s.t. \(f_G(1_S) \leq O(\sqrt{\epsilon} \mu(S)\).
Cor: If \(\mu(\{ i : x_i \gt 0 \}) \leq \delta\) then set measure \(\leq \delta\).
Soft Cheeger’s Inequality: (Dimitriou-Impagliazzo) If \({\| x \|}_1 \leq \sqrt{\delta n}{\| x \|}_2\) then there is \(S\) of measure at most \(O(\sqrt{\delta} n)\) s.t. \(f_G(S) \leq O(\sqrt{\epsilon})\mu(S)\).
Proof: Split \(x = x' + x''\) where \(x'\) “large” coords and \(x''\) “small”.
\(x'_i = x_i\) if \(|x_i| \gt {\| x \|}_2/(2\sqrt{n})\), \(x'_i=0\) otherwise.
\({\| x' \|}^2 \geq {\| x \|}^2/2\) and \(f_G(x') \leq f_G(x) \leq \epsilon 2{\| x' \|}^2\)
But \(|\{ i : x'_i \neq 0 \}| \leq 2\sqrt{\delta} n\)
∎
Proof of structure thm
Reduces structure theorem to following:
Thm: If \(\lambda_{n^\beta} \lt \epsilon\) then \(\exists\) \(x\) s.t. \(f_G(x) \leq O(\epsilon/\beta)\mu(x)\) and \({\| x \|}_1 \leq {\| x \|}_2\sqrt{n^{1-\beta/2}}\).
Proof of main technical thm
Proof: Let \(\Pi\) be projector to \(v_1,\ldots,v_{n^\beta}\). \(Tr(\Pi) = n^\beta\). Assume \(e_1^\top \Pi e_1 \geq n^{\beta-1}\)
\(w\in \Pi \color{red}{\Rightarrow} w^\top A_G w \geq (1-\epsilon){\| w \|}^2\)
\(v_t\) := dist of \(t\) step “lazy random walk” from \(1\). (\(v_t = \left(\tfrac{1}{2}I+\tfrac{1}{2}A_G\right)^t e_i\))
\({\| v_t \|}_2^2 \geq n^{\beta-1}(1-\epsilon)^t\), \({\| v_t \|}_1=1\)
Find \(t \leq 0.1\beta \log n/\epsilon\) s.t. \({\| v_t \|}/{\| v_{t-1} \|} \geq 1- O(\epsilon/\beta)\) ∎
SOS formulation of ABS
Thm: (Arora-B-S) Can solve \(SSE(\epsilon)\) in \(\exp(n^{O(\epsilon)})\) time.
Thm: (B-Raghavendra-S) Do so via \(n^{O(\epsilon)}\) degree SOS.
Proof: By structure thm, every pseudo-dist (over unit vectors) will have \({\tilde{\mathbb{E}}}{\| \Pi x \|}^2 \geq 0.99\).
use
Fix vector in subspace thm: If \(\mu\) is degree \(O(d)\) over unit vecs dimension \(d\) subspace \(V\) and \(w\) random Gaussian in \(V\), then \({\tilde{\mathbb{E}}}_{v\sim \mu} {\langle w,v \rangle}^{O(d)} vv^\top\) has \(\sim\) rank one.
From SSE to UG
Expander partitioning lemma: (Leighton-Rao) By removing \(0.01\) fraction of edges, can decompose every graph into disjoint collection of graphs with \(\lambda_2 \gt \Omega(1/\log^2 n)\)
Proof: Apply Cheeger recursively.
SSE partitioning lemma: (Arora-B-S) By removing \(0.01\) fraction of edges, can decompose every graph into disjoint collection of graphs with \(\lambda_{n^{O(\epsilon^{1/3})}} \gt \Omega(\epsilon)\)
Proof: Apply structure theorem recursively.
Corollary: Enough to solve \(UG(\epsilon)\) in \(\exp(O(m))\) time for graphs where \(\lambda_m \geq 1000\epsilon\).
Can be done via “fix vector in subspace thm”
Can algorithms be improved?
Question: Suppose \(\varphi_G(\delta) \rightarrow 1\) when \(\delta\rightarrow 0\). What’s largest \(m\) s.t. \(\lambda_m \lt 0.01\)?
Running time of algorithm is \(\exp(m)\).
Example: Noisy cube: \(V_G = {\{0,1\}}^{\log n}\), \(x \sim y\) if \(\Delta(x,y) \leq 0.01\log n\). \(\log n\) eigenvalues of valuse \(0.01\). If \(\mu(S) = 2^{-t}\) then \(f_G(x) \geq (1-0.99^t)\mu(x)\).
Short code graph: (B-Gopalan-Hastad-Meka-Raghavendra-S’11) \(V_G = \{ p:{\mathbb{F}}_2^\ell\to{\mathbb{F}}\;|\; \deg(p)\leq d \}\). \(n=2^{\ell^d}\). \(p \sim q\) iff \(p-q=\alpha(x)^d\). \(\ell = \exp((\log n)^{1/d})\) eigenvalues of value \(1-2^{-d}\) s.t. if \(\delta=o(1)\) then \(\varphi_G(\delta)\geq 1-2^{-2^d}-o(1)\).
Proof is obtained by reduction to testing of Reed Muller code (Bhattacharyya-Kopparty-Schoenebeck-Sudan-Zuckerman’10)
The state of art
Short code: “Almost (sub)exponential” lower bound for ARV algorithm
SOS Strikes back: Degree \(16\) SOS can certify SSE of the short code! (B-Brandao-Harrow-Kelner-Steurer-Zhou’12)
From quantum with love: Good enough algorithms for identifying entanglement could refute small set expansion, speed up ABS. (B-Brandao-Harrow-Kelner-Steurer-Zhou’12, B-Kothari-S’17)
Latest updates
Revenge of the games: Candidate NP hardness for \(0.5\) vs \(o(1)\) unique games, “based” on degree two short code. (Dinur-Khot-Kindler-Minzer-Safra’16)
Informally/morally: “Inverse conjecture for short code”: if \(f_{SC}(1_S) \leq (1-\epsilon)\mu(S)\), then \(S\) is \(\Omega_\epsilon(1)\) correlated with “simple” affine subspace of \({\mathbb{F}}_2^{n\times n}\).
Recap
Grand challenge: Characterize function \(\xi(P,s,c)\) mapping predicate \(P\) and \(c \gt s\) to \(\xi\) s.t. \(CSP(P)_{c \text{ vs } s}\) is solveable in \(\exp(n^{\xi})\).
(assuming ETH)
UGC: \(\xi(UG,1-\epsilon,\epsilon)\gt0\)
Raghavendra’s Thm: UGC implies for every predicate \(P\), \(\xi(P,s,c)=0\) iff degree \(2\) SOS (+ lin constraints) solves \(CSP(P)_{c+o(1) \text{ vs } s-o(1)}\).
Conjecture: \(\xi(P,s,c) \sim \log_n deg_SOS(CSP(P))_{c \text{ vs } s}\)
